1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73
| import numpy as np from scipy import linalg import pandas as pd def qr(A): n, m = A.shape R = A.copy() Q = np.eye(n) for k in range(m-1): x = np.zeros((n, 1)) x[k:, 0] = R[k:, k] v = x v[k] = x[k] + np.sign(x[k,0]) * np.linalg.norm(x) s = np.linalg.norm(v) if s != 0: u = v / s R -= 2 * np.dot(u, np.dot(u.T, R)) Q -= 2 * np.dot(u, np.dot(u.T, Q)) Q = Q.T return Q, R def mySweep(A, m): B = np.copy(A) n = B.shape[0] for k in range(m): for i in range(n): for j in range(n): if i != k and j != k: B[i,j] = B[i,j]- B[i,k]*B[k,j]/B[k,k] for i in range(n): if i != k: B[i,k] = B[i,k]/B[k,k] for j in range(n): if j != k: B[k,j] = B[k,j]/B[k,k] B[k,k] = - 1/B[k,k] return B def mylm1(X,Y): n, m = X.shape Z = np.hstack((np.ones(n).reshape((n, 1)), X, Y.reshape((n, 1)))) A = np.dot(Z.T, Z) S = mySweep(A,m+1) beta_hat = S[0:m+1, m+1] return beta_hat def mylm2(X,Y): n, m = X.shape Z = np.hstack((np.ones(n).reshape((n, 1)), X, Y.reshape((n, 1)))) _, R = qr(Z) R1 = R[:m+1, :m+1] Y1 = R[:m+1, m+1] beta = np.linalg.solve(R1, Y1) return beta A = pd.read_csv(r"C:\Users\Nicky\Documents\state_x77.csv") X = A.loc[:,['Population','Income','Illiteracy','Murder','HS.Grad','Frost','Area','Density']].values Y = A.loc[:,['Life.Exp']].values mybeta1 = mylm1(X,Y) print(mybeta1) mybeta2 = mylm2(X,Y) print(mybeta2) Z = np.hstack((np.ones(X.shape[0]).reshape((X.shape[0], 1)),X)) w = linalg.lstsq(Z,Y)[0] w = w.reshape(1,X.shape[1]+1) print(w)
|
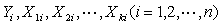 ,写成方程组的形式为:
,写成方程组的形式为: