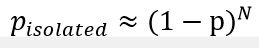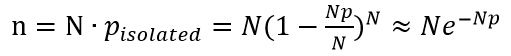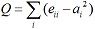盒子
盒子

R包igraph的使用

2016.04.06 nichunquan machine learning  热度 ℃

python 和 R 中都有 igraph 这个包，但看到网上说python中缺少部分函数（比如aging method），所以本文使用R对igraph里面的部分函数做下实验。顺便学习下关于图论里面的一些定理

####1.生成一个1000个节点的无向随机图，边概率分别是0.01,0.05,0.1:（就是任意两个节点间有边的概率），判断这些图是不是连通图，并求其直径。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
library(igraph)
p <- c(0.01,0.05,0.1)
sig <- c(1,1,1)
col <-c("red","green","blue")
for(i in 1:3){
  for(j in 1:100){
    graph<-erdos.renyi.game(1000,p[i])
    if(sig[i]){
      d<-degree.distribution(graph)
      sig[i] = 0
    }else{
      d<- d + degree.distribution(graph)
    }
  }
  d = d/100
  plot(d, type="o", col=col[i],main=paste("Density function for graph",i,"(with p=",p[i],")"),xlab="degree",ylab="Probability Density")
 
}
	
connect_ <- c(0,0,0)
diameter_ <- c(0,0,0)
for(i in 1:3){
  for(j in 1:100){
    graph<-erdos.renyi.game(1000,p[i])
    if(is.connected(graph)){connect_[i]=connect_[i]+1}
    diameter_[i] = diameter_[i]+ diameter(graph)
  }
  diameter_[i] =  diameter_[i]/100
  connect_[i] = connect_[i]/100
  cat("when p =", p[i],",it has probability ",connect_[i],"the network is connected. ")
  cat("Diameter for this network: ",diameter_[i],'\n')
}
when p = 0.01 ,it has probability  0.93 the network is connected. Diameter for this network:  5.38 
when p = 0.05 ,it has probability  1 the network is connected. Diameter for this network:  3 
when p = 0.1 ,it has probability  1 the network is connected. Diameter for this network:  3

1
1
1

erdos.renyi.game() 就是这样一个随机构造图的函数，第一个参数是顶点个数，第二个参数可以是一个概率（表示随机两点之间有边的概率）或者是一个整数值，表示总共有多少条边，还有一个默认参数directed = FALSE，如果为TRUE则是有向图。

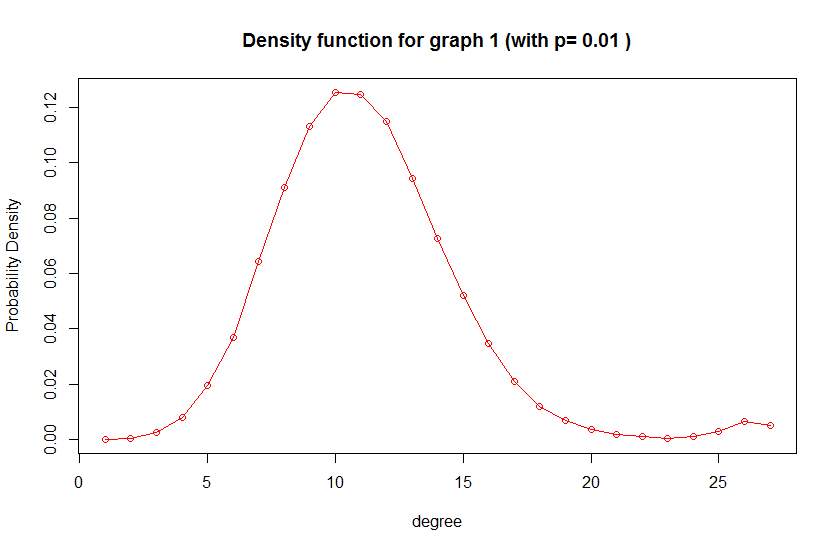
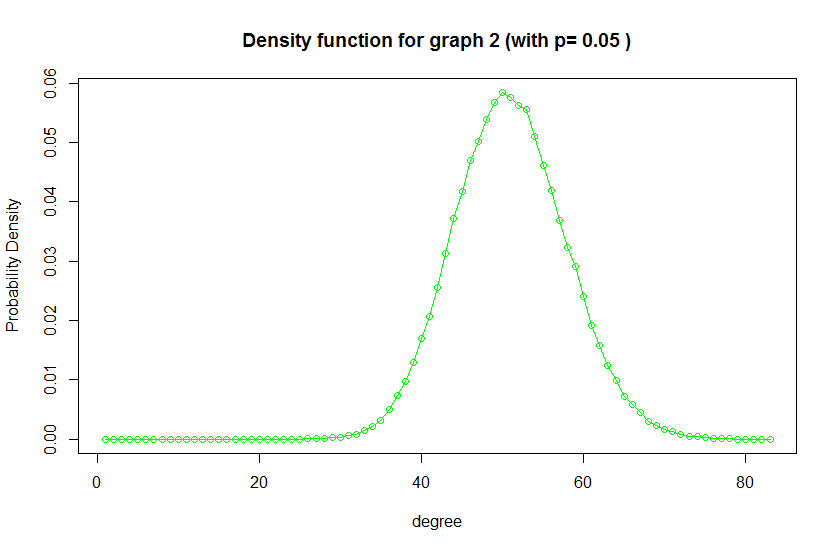
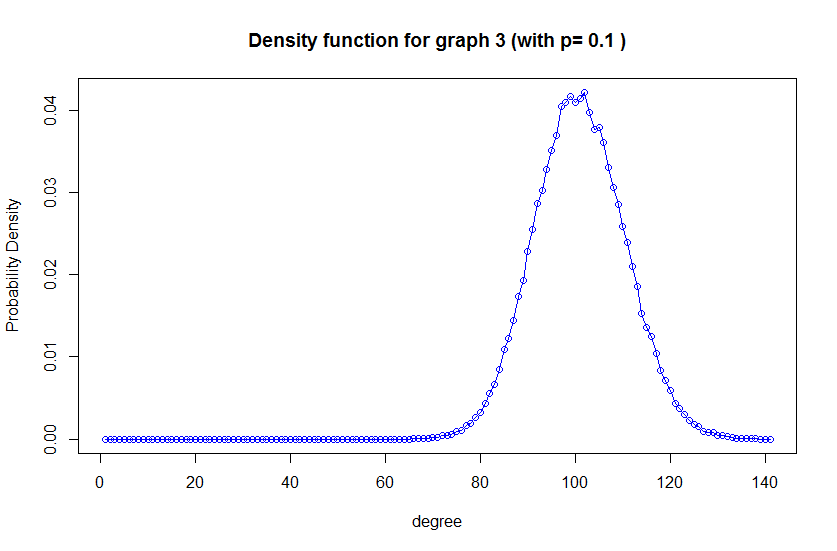
degree.distribution() 就是求一个图中度的分布函数如上面三幅图可见一般度就集中在N*P那边。

is.connected() 和 diameter() 分别求图是否是连通图，以及图的半径。

对这个做一个延伸，到底什么时候这个网络是不连通的呢？看到当p = 0.01时并不是所有的图都是连通的了，那有没有一个具体的值，使得当P>Pr时，是连通图，P<Pr时是非连通图？

这里我们用代码去夹逼这个值，我们从0.05作为初始值，以0.0001为步长，不断去计算连通性，计算出临界值，重复50次

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
p = 0.05     
	p_c = 0
	iter = 0.0001
	for(i in 1:50){
	  while(1){
	    graph<-erdos.renyi.game(1000,p)
	    if(is.connected(graph)){
	      p = p - iter
	    }else{
	      p_c = p_c + p
	      break
	    }
	  }
	}
	p_c = p_c /50
	
	cat("when p < ",p_c,"the generated random networks are disconnected, and when p > ",p_c,"the generated random networks are connected")
when p <  0.006976 the generated random networks are disconnected, and when p >  0.006976 the generated random networks are connected

那么这个值究竟是不是定的，以及是怎么定下来的？

可以参考随机图的维基百科，可以看到这个定值其实就是ln(N)/N 所以这里N=1000结果就是 0.00691 和刚刚模拟的 0.006976 很相近，这个ln(N)/N 是如何得来的？

首先孤立点的概率是1

然后求孤立点个数的表达式，并令N趋于无穷可以得到2

这里在令n=1即可得到P的值为ln(N)/N

####2.生成一个1000个节点的长尾分布图，判断这些图是不是连通图，并求其直径。

这里我们要使用一个函数 barabasi.game() 这个函数是一个叫 Barabasi-Albert模型的实现，是1999年发表在science上的一篇文章提出的一种随机图生成方法，主要见于电影演员的人际关系网、万维网的网页和美国西部电力节点网等等。有时这种网络又称作无标度网络。服从的是幂律的分布。
这种网络的特点是：

成长性：有别于节点数量固定的方式，BA模型从一张小的网络图开始，逐渐增加节点。

优先连接性：每当一条新的边被创建，它总是更倾向于连接度数很大的节点，这种 “马太效应” 正是许多实践网络的特征。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
library("igraph")
graph<- barabasi.game(1000,directed=FALSE)
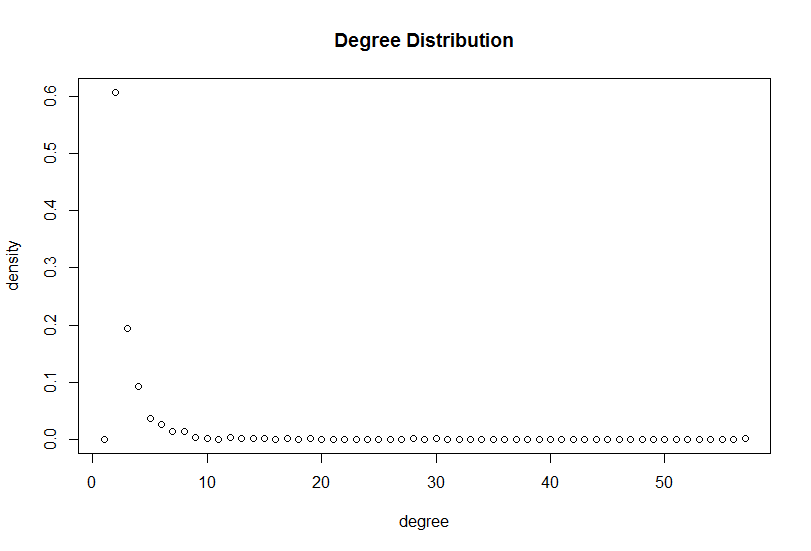
d<-degree.distribution(graph)
plot(d, main='Degree Distribution',xlab="degree",ylab="density")
connectedness=diameter_=numeric(0)
for (i in 1:100){
  g = barabasi.game(1000,directed=FALSE)
  connectedness = c(connectedness, is.connected(g))
  diameter_ = c(diameter_, diameter(g))
}
Dia_avg = mean(diameter_)
cat("the average diameter of network is",Dia_avg,'\n')
con_avg = mean(connectedness)
cat("it has probability ",con_avg ,"the network is connected.",'\n')

1

the average diameter of network is 20.11 
it has probability  1 the network is connected. 

1
2
3
4
struct = fastgreedy.community(graph)
mod = modularity(struct)
cat("the modularity of this 1000 nodes network is ",mod,'\n')
the modularity of this 1000 nodes network is  0.9334264

这里主要看igraph里面的两个函数 fastgreedy.community() 和 modularity()
前一个函数是使用快速贪心算法来进行 社区发现 其实社区发现是一个聚类算法，一般有用GN分裂算法划分网络社团。
后一个函数定义为图中所有连接社团内部边的比例与社团间连边的比例的差值。这里的Q定义为 ：

我们直观地看下由 barabasi.game() 生成的图，可见确实其社区内部边较为密集，而社区之间的边稀疏。